Here is what I was taught in my data structure class.
- Vector runs in O(n) for find, insert, and erase. O(1) if you only insert and erase at the end. O(1) for random access.
- Map uses a balanced tree structure and runs in O(log n) for find, insert, and erase.
- There is a constant k in front of the big-O notation. Since k is a constant, O(log n) will beat O(n) after some value of n.
But is it really that simple?
Not So Constant
In Cliff Click’s video on modern hardware, he showed that latency from cache misses is the dominating factor in today’s software performance.
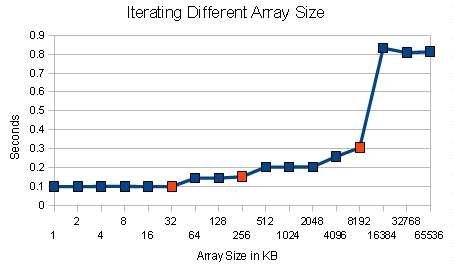
To show this, we can write up a simple function that performs linear search on different sizes of arrays. To keep it fair, we will loop back to the beginning of the array to normalize the number of iterations.
struct OneKBChunk // 1KB, no padding
{
int key;
char buffer[1020];
};
bool LinearFind(unsigned int kBytes)
{
OneKBChunk * chunks = new OneKBChunk[kBytes]; //array of 1KB chunks
bool found = false;
int index = 0;
for(unsigned int i=0; i<10000000; ++i) //arbitrary value
{
// prevent compiler from optimizing away the loop
if(chunks[index].key == 0xdeadbeef)
found = true;
// loop back to the beginning of the array
++index;
if(index >= kBytes)
index = 0;
}
delete [] chunks;
return found;
}
Here are the timing on various array sizes.
The processor on my machine is an Intel I5-750. It is a quad-core processor with 32KB of L1, 256 KB of L2, and 8MB of L3.
The graph demonstrates the penalty on different level of cache misses.
We know that linear search runs in k*O(n). In reality, k really depends on n.
Map and Cache Misses
As Raymond Chen said, vector is about the most cache friendly data structure out there. Trees like data structure uses pointers heavily, and have horrible cache locality.
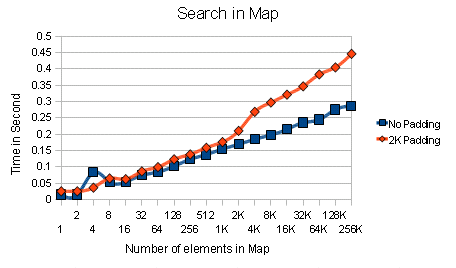
To see the impact of poor cache locality, here is an example that searches the map.
The program is run twice, once without padding, and another with 2KB padding between each insertion. The padding is used to create some distance between each item inserted into the map.
void MapFind(unsigned int kBytes, int timesToRun)
{
std::map<int, OneKBChunk *> chunks;
//std::vector<OneKBChunk*> padding;
for(unsigned int n=0; n<kBytes; ++n)
{
chunks.insert(std::make_pair(n, new OneKBChunk));
//2KB padding in between each insert to the tree
//for(unsigned int p=0; p<2; ++p)
// padding.push_back(new OneKBChunk);
}
// run find() arbitrary number of times
for(unsigned int i=0; i<timesToRun; ++i)
chunks.find(0xdeadbeef);
// .. delete padding here
}
The elements of the maps in both run are identical, and were run in same number of iterations.
Again, similar to the example before, the constant k isn’t really constant.
In reality, the cache misses with map are far more unpredictable than my simple example. As the program runs longer, the items in the map could end up very far apart in memory.
Conclusion
The constant k includes cache effects, which is not nearly as constant as as how I was taught in my data structure class.
On a side note, my Computer Architecture professor once said “The understanding of cache locality will determine whether you are a $50K programmer or a $100K programmer (2002 dollar)”.
Source
The source and the spreadsheet can be downloaded here.
That javaone talk was pretty nuts. He makes a good point on how freaken complicated modern processors are and have been for a while.
From an algorithm complexity standpoint, the textbook answers are still correct. The performance degradation is due to a hardware implementation issue – the lack of magic memory that is infinitely large and instantaneous. The way cache hit and misses are dealt with vary from processor to processor. So unless you are writing code for a specific processor, I would be careful about how much time is spent optimizing for cache locality.(some may evict the least recently used entry, most recently used, least FREQUENTLY used, processors also have different cache associativity, etc)
Also have you looked to see the effects on performance when the vector needs items inserted? The insertion of items into the vector would invalidate the previous cache entries causing more cache misses until it repopulates the cache – especially when it grows large enough and needs to dynamically reallocate more memory to store the additional entries. But then again, maybe that penalty will be amortized in the long run?
Anyway, this is interesting, I wonder what hardware designers can do to optimize cache algorithms for the map data structure.
Of course, in the computer science discipline, the textbook is correct. But in the field of software engineering, the textbook is misleading.
I am not saying that we should optimize for specific processor. After all, premature optimization is the root of all evil. Rather, I just want to point how that the constant that we were taught in data structure courses is not constant in practice. In fact, when pointers are used (such as tree), it is highly unpredictable.
For vector, you can easily avoid the reallocation through reserve() or resize(). Chances are you will have some idea the maximum size the vector will be. In practice, I almost always reserve() on vector.
Amortized runtime is something I pay special attention to. It is basically saying that in the long run, things will average out. But like Keynes once said, “In the long run, we are all dead”. How long is this long run?
There are cache friendly tree data structure out there. Structure such as a heapified vector (make_heap()) is fast, and should have good cache locality if implemented properly.
Just give us infinite fast memory, problem solved. 🙂